树状数组 - Durjustice's Site

前言#

这篇文章我将从我两周前完成的一道算法题出发，介绍我关于树状数组的学习和理解，最后再谈谈其所引起的一些感受。

题目#

社团活动一共有 $n$ 个项目，第 $i$ 个项目将于第 $l_i$ 到第 $r_i$ 天进行。社团中有 $m$ 个社员，第 $j$ 位社员将在第 $a_j$ 到第 $b_j$ 天有时间参加项目，一位社员每天可以参加多个项目。求每位社员最多能完整完成几个项目。
输入格式：
第一行包含两个整数 $n,m$ ，分别代表项目的数量和社员的数量( $1 \leq n, m \leq 10^5$ );
接下来的 $n$ 行，第 $i$ 行有两个整数 $l_i,r_i$ ，代表第 $i$ 个项目的时间( $1 \leq l_i \leq r_i \leq 10^5$ );
接下来的 $m$ 行，第 $j$ 行有两个整数 $a_j,b_j$ ，代表第 $j$ 个社员的时间( $1 \leq a_j \leq b_j \leq 10^5$ )。
输出格式：
输出 $m$ 行，第 $i$ 行输出一个整数，代表第 $i$ 个社员最多完整完成的项目数量。

题意很容易理解，可以设想一条时间轴，每个社员和项目都对应一段时间区间，我们需要处理区间包含关系，计算每个社员的时间区间内包含了多少个完整的项目区间。

直观思路#

最直观的解法是枚举每个社员和项目的组合。对第 $i$ 个项目和第 $j$ 个社员，如果满足 $a_j \leq l_i \leq r_i \leq b_j$ ，那么该社员可以完整参加这个项目。对每个社员统计满足条件的项目即可得到答案。对于这个算法：

正确性(correctness)：无疑是正确的
效率(efficiency)：时间复杂度是 $O(mn)$ ，不优

启发和思考#

直观的解法带来一个启发，我们似乎不能将每个社员单独拿出来考虑，因为对每个社员你都必须检查每个项目，会得到同样的时间复杂度。那么就应该考虑整体，而整体的属性无非就是大小关系了。

另一种可能的思路是，我们可以处理完所有项目之后，再根据得到处理结果考虑每个社员，这样的话效率可能会更好。这里先按下不表。

顺着前一种思路继续思考，我们无法对区间进行有效的排序方法，所以只能根据区间一端的大小进行排序，但这也是很大的进步。不妨根据区间左端点排序，这样就可以将注意力集中在区间右端点的处理上。

优化效率#

第一个尝试是将社员和项目分开排序，然后使用双指针技巧处理（类似归并排序中的合并操作）。试着想一想会发现这不是可行的思路，因为对于每一个社员，还是需要考虑所有左端点不小于社员左端点的项目，再通过右端的比较判断能否完成项目，并没有本质上改善时间复杂度。

于是尝试统一处理社员和项目，将它们放在一个数组内一起排序。事实上二者的属性是一致的，所以定义如下的类：

class Project:
    def __init__(self, left, right, is_project, idx):
        self.l = left
        self.r = right
        self.is_project = is_project  # True表示项目，False表示社员
        self.index = idx       # 原始下标

根据区间一段排序后，我们想得到的效果是，遍历时不需要再考虑一端的因素。进而可以想到，根据左端点降序排列（相等时项目排在社员前），依次访问每个元素，这样在遍历时就能保证，当遇到一个社员时，后面未处理的项目的左端点一定不满足条件。

# 按左端点降序排序，左端点相同时项目优先
events.sort(key=lambda x: (-x.l, not x.is_project))

那么我们可以自然地得到这样的算法：在遍历排序后的事件时，维护一个时间轴，记录社员以每个时间点作为右端时，可以完整参加的项目数量。当遇到项目时，更新时间轴；当遇到社员时，查询其右端点的累计值。

ans = [0] * m
count = [0] * max_b    # max_b为最大的社员时间区间右端点 
for event in events:
	if event.is_project:
		for i in range(event.r, max_b+1):
			count[i] += 1    # 不小于项目右端点的时间点加1
	else:
		ans[event.index] = count[event.r]

但是，问题出现在了对数组元素的处理上。处理一个社员的时间复杂度是 $O(1)$ ，但是处理一个项目的时间复杂度是 $O(max\_b)$ ，那么处理整个已排序数组的时间复杂度就是 $O(n \times max\_b)$ 。尽管已经优化了很多，在某些极端情况下（比如所有项目都集中在时间轴的前端），这个复杂度仍然不够理想。

为了解决该问题，我们引入树状数组。

树状数组#

树状数组（Binary Indexed Tree，BIT）是一种用于高效处理数组前缀和的数据结构。它支持两种基本操作：

单点修改：修改数组中某一个位置的值
区间查询：查询数组中某个区间的和

这两种操作的时间复杂度都是 $O(\log n)$ ，这使得它在处理需要频繁修改和查询的场景中特别有用。

引入#

先解释一下什么是单点修改和区间查询，以前面的算法为例：

单点修改：处理项目，更新时间轴， $O(max\_b)$
区间查询：处理社员，查询右端点累计值， $O(1)$

当然你可以这样改变原先的算法：

count = [0] * max_r    # max_r为最大的项目时间区间右端点，防止报错
for event in events:
	if event.is_project:
		count[event.r] += 1
	else:
		for i in range(event.l, event.r+1):
		ans[event.index] += count[i]

单点修改：处理项目，设置右端点处个数加1， $O(1)$
区间查询：处理社员，计算时间区间内个数和， $O(max\_b)$

这就是用普通数组处理区间内元素求和问题上两种不同角度，或者说不同次序的方法。

思想#

我的理解是，我们有一个原始数组 $a$ ，想要计算其某一区间上的和，直接计算复杂度肯定与区间长度有关。所以想要一个新的数组 $c$ ，每个元素都存储 $a$ 中某个特定区间中的元素之和，这样就可以减少计算，例如

$\sum_{i=1}^7 a[i] = \sum_{i=1}^4 a[i] +(a[5]+a[6]) + a[7] = c[4] + c[6] + c[7]$

但是这样会带来副作用，即在更新 $a[i]$ 时，需要更新所有包含 $a[i]$ 的 $c[j]$ 。而树状数组利用二进制的结构，很好地将两个操作的复杂度平衡在 $O(\log n)$ ，令人不由慨叹数据结构的巧妙。

结构#

BIT

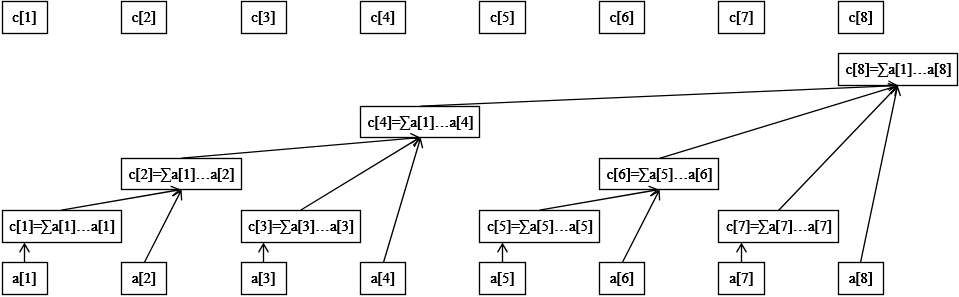
树状数组中 $c[x]$ 维护的区间长度为 lowbit(x)。

NOTE
lowbit操作是树状数组的基础，它返回一个数字的二进制表示中最低位1所代表的值。
def lowbit(x):
    return x & (-x)
例如 $lowbit(8) = lowbit(1000_2) = 1000_2 = 8$ 。如果你熟悉有符号整型的二进制表示，上面的代码并不难理解，便不再赘述。

$c[x]$ 维护的是 $[x-lowbit(x)+1, x]$ 的和，即

$t=x-lowbit(x)+1 \text{, } c[x] = \sum_{i = t}^x a[i]$

操作#

你会发现在树状数组中，修改 $a[x]$ 的值时所要修改的 $c$ 中的元素，有且仅有一个会出现在，查询上限不小于 $x$ 的前缀和时，对应的 $c$ 中的元素中。这就确保了正确性，建议结合示意图和例子进行理解。

单点修改#

当我们要修改原始数组位置 $x$ 的值时，需要修改所有包含该位置的区间和：

def update(pos, val):
    while pos <= n:
        c[pos] += val
        pos += lowbit(pos)

在图上表现为从当前顶点向根的方向依次修改，因为 $c[x]$ 真包含于 $c[x+lowbit(x)]$

例如更新位置3的值时，需要依次更新

$3 = 0011_2 \rightarrow 0100_2 \rightarrow 1000_2$

c[3]（包含a[3]）
c[4]（包含a[1:4]）
c[8]（包含a[1:8]）

区间查询#

查询前缀和（ $1$ 到 $pos$ 的和）的过程是单点修改的逆过程：

def query(pos):
    total = 0
    while pos > 0:
        total += c[pos]
        pos -= lowbit(pos)
    return total

在图上表现为当前顶点向左邻的分支上依次查询，因为对于任意 $x<y<x+lowbit(x)$ 有 $c[x]$ 和 $c[y]$ 不相交，同时对于任意 $c[x]$ 和 $c[y]$ 要么不相交要么一者包含另一者。

例如查询1到7的和时

$7 = 0111_2 \rightarrow 0110_2 \rightarrow 0100_2$

$\sum_{i=1}^7a[i] = c[7] + c[6] + c[4]$

求区间 $[l, r]$ 上的元素和时，只需要：

ans = query(r) - bit.query(l - 1)

回到题目#

以上就是关于树状数组的基本内容，理解了它的原理之后，先前的困难便迎刃而解。在给出解答之前：

还记得用普通数组处理区间元素求和问题的两种角度吗？树状数组很像是介于两者之间，你可以从两种角度来理解它所实现的优化，都是将两个操作极端的时间复杂度 $O(max\_b)$ 和 $O(1)$ 平衡为两个都为 $O(\log max\_b)$ 。

此外，你还记得“启发和思考”中提到的“先处理项目，再处理社员”的思路吗？在有了树状数组这个强大的数据结构后，最初的将区间一端排序的优化也显得没那么重要了。试着用树状数组直接解决这个问题！该思路和文中主要阐述的思路整体时间复杂度都为 $O((n+m)\log max\_b)$ 。

最后给出题目的解答：

class BIT:
    def __init__(self, n):
        self.size = n
        self.tree = [0] * (n + 1)
    
    def _lowbit(self, x):
        return x & (-x)
    
    def update(self, pos, val):
        while pos <= self.size:
            self.tree[pos] += val
            pos += self._lowbit(pos)
    
    def query(self, pos):
        total = 0
        while pos > 0:
            total += self.tree[pos]
            pos -= self._lowbit(pos)
        return total

class Project:
    def __init__(self, left, right, is_project, idx):
        self.l = left
        self.r = right
        self.is_project = is_project  # True表示项目，False表示社员
        self.index = idx       # 原始下标

def solve():
    n, m = map(int, input().split())
    
    events = []
    max_b = 0        # 当然你可以直接用 MAXN = 100010
    # 读入项目信息
    for i in range(n):
        l, r = map(int, input().split())
        events.append(Project(l, r, True, i))
    
    # 读入社员信息
    for i in range(m):
        a, b = map(int, input().split())
        events.append(Project(a, b, False, i))
        max_b = max(max_b, b)
    
    events.sort(key=lambda x: (-x.r, not x.is_project))
    
    bit = BIT(max_b)
    ans = [0] * m
    # 从右到左扫描
    for event in events:
        if event.is_project:
            # 如果是项目，在左端点位置加1
            bit.update(event.r, 1)
        else:
            # 如果是社员，查询区间[event.l, event.r]内的项目数量
            ans[event.index] = bit.query(event.r)  # 直接查询[1, r]即可是排序的作用
    
    for result in ans:
        print(result)

if __name__ == "__main__":
    solve()

题外话#

本文所呈现的其实也是我在第一次做这个题的思考历程，但是那时我并不知道树状数组，于是走到了文中所述的排序优化后便卡壳了。我发现在学了数据结构后，我和大一时一股脑刷洛谷状态是完全不同的，面对一些有挑战的题，我的思路明显变得更有逻辑，而不是见过就会没见过就不会的状态，让我回想起高中学数竞不断积累过后柳暗花明又一村的感受，虽然还不及当年那般强烈就是了。因此尽管当时没做出来，我仍觉得有所收获和感触，而在看了题解、学习了树状数组后，我更是慨叹于其构造的美妙，所以也才有了这篇文章。要说我痴迷于数据结构，或是数学吗？也不尽然，我想这是本就属于它们的魅力所在。

在 mit 6.006 2020 的 Problem Session 3 的 P2 如是问道：用黑箱的哈希表如何实现双端序列的操作（Double-Ended Sequence Operations）。换句话说，就是要实现双端队列的操作并且访问节点的复杂度是 $O(1)$ 。你可以回想一下，如何用数组实现双端序列，再想想哈希表和数组有什么联系和区别，我想你就能得出答案了。

总而言之：

切实地感受知识的调用和链接，妙处难于君说。

外部链接#

OI-wiki 树状数组